La sorprendente constante de Khinchin
Las matemáticas nunca dejarán de sorprenderme. En cualquier lugar puedes encontrarte una cuestión interesante, una relación curiosa o una propiedad inesperada de algún número, alguna función o alguna figura. Particularmente conozco un buen número de ejemplos de este tipo (muchos de ellos os los he comentado en este blog), y en este post vamos a añadir uno más a la lista: la constante de Khinchin.
Vamos a comenzar presentando esta constante de Khinchin. Es la siguiente:
Vamos a comenzar presentando esta constante de Khinchin. Es la siguiente:
Para poder explicar de dónde sale dicho número y hablar sobre sus propiedades necesitamos antes recordar algunas cosas sobre fracciones continuas. Una fracción continua es una expresión del tipo siguiente:
donde 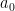 es un número entero y
es un número entero y  son números enteros positivos. Suele abreviarse de la forma
son números enteros positivos. Suele abreviarse de la forma ![[a_0;a_1, \ldots , a_n, \ldots ] [a_0;a_1, \ldots , a_n, \ldots ]](https://s0.wp.com/latex.php?latex=%5Ba_0;a_1,+%5Cldots+,+a_n,+%5Cldots+%5D&bg=ffffff&fg=000000&s=0) (la expresión podría ser finita o infinita).
(la expresión podría ser finita o infinita).
Como podéis ver, en la expresión anterior todos los numeradores son 1, pero seguro que en alguna ocasión habéis visto una fracción continua con otros números en el numerador. Bien, cuando todos son 1 la fracción continua se llama regular, y cuando permitimos otros números se denomina generalizada. En este post podéis encontrar más información sobre ellas, en este otro tenéis fracciones continuas de números muy conocidos y aquí una interpretación combinatoria de las mismas.
Una de las principales propiedades de las fracciones continuas es que todo número real puede expresarse como una fracción continua regular. Es decir, podemos expresar todo número real de la forma ![[a_0;a_1, \ldots, a_n, \ldots ] [a_0;a_1, \ldots, a_n, \ldots ]](https://s0.wp.com/latex.php?latex=%5Ba_0;a_1,+%5Cldots,+a_n,+%5Cldots+%5D&bg=ffffff&fg=000000&s=0) . Olvidémonos de
. Olvidémonos de 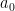 y quedémonos con los
y quedémonos con los  desde
desde 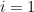 hasta
hasta  . Ahora calculemos la media geométrica de esos términos, es decir:
. Ahora calculemos la media geométrica de esos términos, es decir:
y después el límite de esa expresión cuando  a infinito. Entonces, casi siempre ocurre lo siguiente:
a infinito. Entonces, casi siempre ocurre lo siguiente:
Es decir, el límite de la media geométrica de los  desde
desde 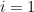 hasta
hasta  casi siempre (esto es, para casi todos los números reales) vale
casi siempre (esto es, para casi todos los números reales) vale 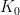 , la constante de Khinchin. Tremendo, ¿verdad?
, la constante de Khinchin. Tremendo, ¿verdad?

Este resultado lo demostró Aleksandr Khinchin (en ocasiones escritoKhintchine), matemático soviético de la primera mitad del siglo XX (nació en 1894 y murió en 1959) que trabajó en múltiples áreas de las matemáticas y la física: análisis real, teoría de la probabilidad, teoría de números o física estadística. Podéis encontrar más información sobre él aquí y aquí (web de la que he tomado la foto de Khinchin).
Bien, posiblemente la primera pregunta que os ha surgido a la mayoría de los que habéis leído hasta aquí es ésta: ¿qué significa eso de casi siempre? Pues significa, como comenté antes, para casi todos los números reales. Y ese casi lo que nos dice es que el conjunto de números para los cuales no se cumple la propiedad anterior es un conjunto de medida nula, que viene a ser un conjunto que aunque puede ser infinito (como veremos que ocurre en este caso) tiene muy pocos elementos.
Es interesante destacar que aunque esta propiedad la cumplen casi todos los números reales no se ha probado para ningún número en concreto (¡¿?!). Lo que sí se conocen son excepciones, es decir, números de los que se sabe que no la cumplen. Por ejemplo, los racionales no cumplen dicha propiedad. Y tampoco algunos números irracionales como el número  , el número áureo
, el número áureo 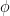 o el número
o el número  .
.
Por otra parte, se conjetura que otros números irracionales (o que se sospecha que lo son) también muy conocidos sí que la cumplen, aunque no se sabe con certeza (recordad que hemos dicho que no se ha demostrado esta propiedad explícitamente para ningún número concreto). Por ejemplo, se cree que el número 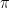 (que sí se sabe quees irracional) cumple esta propiedad, y también la constante de Euler-Mascheroni
(que sí se sabe quees irracional) cumple esta propiedad, y también la constante de Euler-Mascheroni 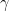 (aunque no se sabe si este número es irracional).
(aunque no se sabe si este número es irracional).
Pero quizás lo más llamativo de todo este tema es que se cree (no está probado, pero los indicios apuntan a ello) que el propio 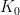 cumple esta propiedad. Es decir, que si expresamos
cumple esta propiedad. Es decir, que si expresamos 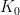 como una fracción continua y calculamos el límite de la media geométrica de los correspondiente valores
como una fracción continua y calculamos el límite de la media geométrica de los correspondiente valores  el resultado sería de nuevo el propio
el resultado sería de nuevo el propio 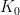 . No sé a vosotros, pero a mí estoy me parecería absolutamente maravilloso.
. No sé a vosotros, pero a mí estoy me parecería absolutamente maravilloso.
Por otra parte, tampoco se sabe si 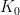 es un número racional, un número irracional algebraico o un número trascendente. Y, por tanto, tampoco si es o no un número normal, aunque también en este caso los indicios apuntan a ello. En la siguiente tabla podéis ver el número de apariciones de los números 0, 1,…,9 en los primeros
es un número racional, un número irracional algebraico o un número trascendente. Y, por tanto, tampoco si es o no un número normal, aunque también en este caso los indicios apuntan a ello. En la siguiente tabla podéis ver el número de apariciones de los números 0, 1,…,9 en los primeros  decimales, para
decimales, para  de 1 a 5:
de 1 a 5:

Como podéis ver, parece que conforme  va siendo mayor la frecuencia de cada uno de los números de una cifra se va pareciendo bastante. Pero lo dicho, no hay ni demostración ni refutación sobre la normalidad de
va siendo mayor la frecuencia de cada uno de los números de una cifra se va pareciendo bastante. Pero lo dicho, no hay ni demostración ni refutación sobre la normalidad de 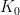 .
.
El límite antes mencionado no es ni mucho menos la única manera de representar 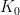 que se conoce. Hay muchas otras que involucran a series infinitas, como ésta:
que se conoce. Hay muchas otras que involucran a series infinitas, como ésta:
Y también se conocen algunas relacionadas con integrales, como ésta:
Y para terminar vamos a responder a una pregunta que posiblemente os habéis hecho muchos de vosotros: ¿por qué se llama a esta constante 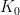 ? Bueno, la
? Bueno, la 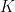 es, como cabía esperar, por ser la inicial de Khinchin. ¿Y el subíndice 0? Pues muy sencillo: porque
es, como cabía esperar, por ser la inicial de Khinchin. ¿Y el subíndice 0? Pues muy sencillo: porque 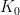 es simplemente un caso particular de una clase de medias de ese tipo,
es simplemente un caso particular de una clase de medias de ese tipo, 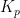 , definidas de la siguiente forma:
, definidas de la siguiente forma:
Se puede demostrar que para  (que sería el caso de la constante de Khinchin) obtenemos
(que sería el caso de la constante de Khinchin) obtenemos 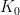 tal cual lo hemos definido al principio de este artículo. Otro valor destacable de esta clase de medias es el que se obtiene para
tal cual lo hemos definido al principio de este artículo. Otro valor destacable de esta clase de medias es el que se obtiene para 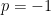 , y que se denomina media armónica de Khinchin:
, y que se denomina media armónica de Khinchin:
Con este artículo sobre la constante de Khinchin espero haberos descubierto algo nuevo, tanto a los que no tenéis muchos conocimientos matemáticos como a los que estáis más metidos en el tema. Para todos, en los enlaces que aparecen debajo de este párrafo podréis encontrar más información sobre esta sorprendente constante.
Fuentes y más información:
- On the Khintchine constant (pdf).
- Khinchin constant’s en la Wikipedia en inglés.
- Khinchin’s constant en MathWorld.
- Khinchin’s constant digits en MathWorld.
- Khinchin’s constant en la OEIS.
- Six sequences, vídeo de los cracks de Numberphile mediante el cual conocí esta constante de Khinchin. En él comentan cosas sobre otras sucesiones que también son interesante.
Esta es la primera contribución de Gaussianos a la Edición 5.7: Alan Turing del Carnaval de Matemáticas, que en esta ocasión tiene como anfitrión a @cuantozombi en su blog El zombi de Schrödinger.
No hay comentarios:
Publicar un comentario